曲线回归分析
一 定义:回归分析(Regression Analysis)是一种统计学上的分析数据的方法,目的在于了解两个或多个变量之间是否相关以及相关方向与强度,并建立数学模型以便观察特定的自变量与需要预测的因变量之间的关系。具体的说,回归分析可以帮助了解在一个或多个自变量变化时因变量的变化量。
二 回归问题的分析方法:1)收集数据;2)建立一个适合相关问题的回归函数;3)通过学习已有的数据,对函数的未知参数进行估计;3)回归方程及回归系数的显著性检验;4)利用这个模型去预测/分类新的数据。
三 回归分析的原理:目的是为了找出一个最能够代表所有观测资料的函数,用这个函数来表示因变量与自变量的关系。回归的基本模型一般可以表示为:Y=f(X ,u),其中Y为因变量,X为自变量,u为未知参数。
四 回归分析方法分类:根据用途可以有多种分类,单变量的线性回归模型,多变量的线性回归模型,广义线性回归模型,概率单位回归模型,逻辑回归模型,曲线回归模型,岭回归模型,主成分回归模型等。
五 回归分析算法背景:
回归分析核心思想是采用最小二乘法原理来求解回归系数,最小二乘法思想背景:1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯计算了谷神星的轨道并进行了分析。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
六 参考资料:
· 中央大学数学系教材-最小二乘法
· 最小二乘法 - 维基百科,自由的百科全书
· http://www.physics.csbsju.edu/stats/least_squares.html
· http://www.orbitals.com/self/least/least.htm
· PlanetMath上最小二乘法
· 马克威分析系统使用教程——http://www.tenly.com
1.1 算法摘要
曲线回归是用来描述变量之间的非线性关系的一种回归模型。通过合适的变换,能够将曲线模型转化为线性模型。可以说非线性回归模型是线性回归的扩展,也是传统计量经济学的一种结构分析模型。
在现实经济生活中,很多现象之间的关系不是线性关系,对这种类型的现象的分析预测一般要应用非线性回归预测,通过变量变换,将非线性的模型转换为线性回归模型。因而,可以用线性回归方法解决非线性回归预测问题。
选择合适的曲线类型不是一件轻而易举的工作,主要依靠专业知识和经验。常用的曲线类型有幂函数、指数函数、抛物线函数、对数函数和S型函数等。
1.2 算法原理
线性回归具有一定的局限性,因为现实中的问题很多属于非线性的关系,要求解这类问题,可以将非线性回归模型转化为线性模型求解。非线性模型的类型有很多种,一般常用的有:抛物线函数、双曲线函数、幂函数、指数函数、对数函数以及多项式方程。常用的非线性方程表达式一般为:
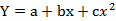 、Y=a+b*(1/X)、Y=a+X1b1+X2b2+…..+Xkbk、Y=abx、Y=a+bln(X)、Y=a+bZ,其中Z=1/X或者Z=lnX。
、Y=a+b*(1/X)、Y=a+X1b1+X2b2+…..+Xkbk、Y=abx、Y=a+bln(X)、Y=a+bZ,其中Z=1/X或者Z=lnX。
将非线性模型转换为线性模型求解,首先要选择适当的非线性回归方程,这个过程可以通过散点图来研究,具体的回归方程为:Y=f(x;a,b),其中a,b分别为回归方程的未知参数。为了求解未知参数的估计值,往往可以先通过变量置换,把非线性回归化为线性回归,再利用线性回归的方法确定参数及b的估计值。下面列举几个常用的曲线模型的变换方式:
| 曲线方程 | 变换公式 | 变换结果 |
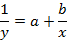
|
X=1/x; | Y=1/y |
| Y=a+bx |
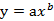
|
X=lnx |
| ; | Y=lny | Y=a’+bX |
| (a’=lnx) | y=a+blnx | X=lnx |
| ; | Y=y | Y=a+bX |
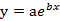
|
X=x; | Y=lny |
| Y=a’+bX | (a’=lnx) |
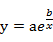
|
| X=1/x; | Y=lny | Y=a’+bX |
线性回归不能解决所有问题,对有的问题可以通过函数的转换,在一定范围内将因变量和自变量的关系变为线性关系;但这种转换可能导致更复杂的计算或者失真;所以可以用曲线拟合的方法,建立简单且合适的模型。
曲线回归的第一步骤是将数据简单的绘制在图形上,并观察数据的分布情况以便确定所应采取的模型。利用曲线估计可以方便地进行线性拟合、增长曲线拟合、指数拟合、对数拟合等。
四参考资料1马克威分析系统使用教程——http://www.tenly.com
五实例示例数据为,在彩色显影中,析出银的光学密度与形成染料的光学密度的试验数据如下:
| x | y |
| 0.05 | 0.1 |
| 0.06 | 0.14 |
| 0.07 | 0.23 |
| 0.1 | 0.37 |
| 0.14 | 0.59 |
| 0.2 | 0.79 |
| 0.25 | 1 |
| 0.31 | 1.12 |
| 0.38 | 1.19 |
| 0.43 | 1.25 |
| 0.47 | 1.29 |
求银的光学密度与形成染料的光学密度的回归方程。
首先判断回归方程的类型,画出数据的散点图:
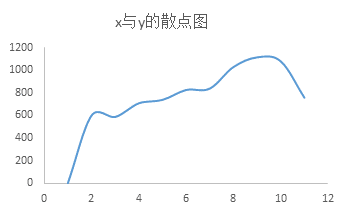
由散点图知,可设回归方程为: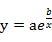 (b<0),其中a和b为参数,对两边取对数则,lny=lna+b/x;作变量代换X=1/x, Y=lny. (A=lna)则上述回归方程变换为:Y=A+bX
(b<0),其中a和b为参数,对两边取对数则,lny=lna+b/x;作变量代换X=1/x, Y=lny. (A=lna)则上述回归方程变换为:Y=A+bX
对数据进行变换,得到的结果如下所示:
| X | Y |
| 20 | -2.303 |
| 16.667 | -1.966 |
| 14.286 | -1.47 |
| 10 | -0.994 |
| 7.143 | -0.528 |
| 5 | -0.236 |
| 4 | 0 |
| 3.226 | 0.113 |
| 2.632 | 0.174 |
| 2.326 | 0.223 |
| 2.218 | 0.255 |
经计算得到: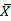 =7.946,
=7.946, ;
;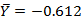 ,
,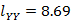 ;
;
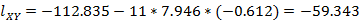
样本的相关系数为:r=-0.998,查表得到,相关系数的绝对值大于临界值,说明Y和X之间的线性相关关系特别显著。再来估计a和b的值。
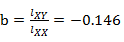 ;
;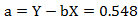
则Y关于X的线性回归方程为:Y=0.548-0.146X;换回原变量得到原始数据的线性回归方程为:
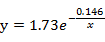 六输入输出
六输入输出
输入变量类型:整型、浮点型(注:自变量可为一个或多个,但因变量只能一个)
输入数据尺度:标量型
输出结果:曲线回归的回归系数,以及回归方程。
七相关条目非线性回归、最小二乘法、变量变换、曲线回归图
八优缺点优点:用线性回归方法解决非线性回归预测问题,而现实中绝大多数的问题均为非线性问题,因此该算法使用范围相对广泛。
缺点:如何选择合适的曲线类型,这是一件有难度的事情,需要依靠专业知识和经验。另外变量转换后会加大计算复杂度和计算量。