配对双样本均值检验
假设检验是用来判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作推断。
假设检验又分为对已知分布的参数检验和对未知分布的非参数检验。参数检验要利用到总体的信息,如总体分布、总体的一些特征和方差;以总体分布和样本信息对总体参数作推断。
参数检验可以分为:以单样本数据的均值推断总体的均值;单样本数据的方差推断总体的方差;以相互独立的双样本数据来推断样本是否来自于同均值或同方差的总体;样本数据的比例检验验证总体数据的比例。
假设检验的基本思想:小概率原理。如果对总体的某种假设是真实的,那么不利于或者不能支持这一假设的事件A(小概率事件)在一次试验中几乎不可能发生的,要是在一次试验中A发生了,就有理由怀疑该假设的真实性,拒绝这一假设。
配对双样本均值检验用于检验两个相关的样本是否来自具有相同均值的总体。进行配对双样本均值检验要求被比较的两个样本具有配对关系,而且均值是对于检验有意义的描述统计量。
进行配对双样本的均值检验目的:判断不同的处理是否有差别;计算的公式及意义:利用T统计量检验,公式为: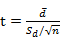 ;自由度:自由度=配对个数-1
;自由度:自由度=配对个数-1
配对样本的均值检验的使用条件:适用于任何领域任意的配对数据;配对样本的均值检验设计:将受试对象的某些重要特征按相近的原则配成对子,目的是消除混杂因素的影响,一是对观察对象之间除了处理因素、研究因素之外,其它因素基本相同,每队中的两个个体随机给予两种处理。
配对样本均值检验的对象包括:1)两种同质对象分别接受两种不同的处理,如性别、年龄、体重、病情程度相同配成对;2)同一受试对象或同一样本的两个部分,分别接受两种不同的处理;3)与自身的对比,即同一受试对象处理前后的结果进行比较。
四参考资料1马克威分析系统使用教程,www.tenly.com
2《应用多元分析(第三版)》,王学民编著,上海财经大学出版社
3《多元统计分析》,张润楚,科学出版社2006年版
五实例示例数据为运动员的跑步成绩,其中T组是未对他们进行体能训练时的成绩,而P组是对他们进行体能训练后的成绩。通过配对双样本均值检验分析体能训练对运动员是否有一定的影响。
| 编号 | T组 | P组 |
| 1 | 1000 | 1600 |
| 2 | 1222 | 1812 |
| 3 | 1221 | 1756 |
| 4 | 998 | 1534 |
| 5 | 1012 | 1567 |
| 6 | 1042 | 1632 |
| 7 | 1004 | 1614 |
| 8 | 1035 | 1639 |
| 9 | 1145 | 1812 |
| 10 | 1121 | 1768 |
将两组数据作为配对数据进行均值检验,现假定原假设为H0:μ1 =μ2;备择假设为H1:μ1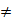 μ2;根据T统计量计算最后得到的结果为:
μ2;根据T统计量计算最后得到的结果为:
统计量:
| 变量名 | 均值 | 频数 | 标准离差 | 均值标准误 |
| T组 | 1,080 | 10 | 90.0272 | 28.4691 |
| p组 | 1,673.4 | 10 | 103.6867 | 32.7886 |
配对样本的相关系:
| 变量名 | 频数 | 相关系数 | P 值 |
| T组-p组 | 10 | 0.9093 | 0.0003 |
配对检验的统计量:
| 变量名 | 差的均值 | 差的标准离差 | 差的均值标准误 | 下限(95.00%置信度) | 上限(95.00%置信度) |
| T组-p组 | -593.4 | 43.3646 | 13.7131 | -624.4212 | -562.3788 |
检验结果:
| 变量名 | 检验的T值 | 自由度 | P值(u1≠u2) |
| T组-p组 | -43.2725 | 9 | 0.0000 |
由统计表可见,运动员的个数为10人,以及他们的两次跑步成绩的均值、频数、标准差和均值标准误。
由相关性表可见,相关系数为0.9093,显著性为0.0003小于0.05,所以T组和P组有相关关系。
由检验结果表可见,因为显著性为0.0000远小于0.05,因此认为体能训练对于运动员的跑步成绩有明显效果。
六输入输出输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
输出结果:统计:列出样本的统计信息。相关性:得到配对检验样本的相关系数,相关系数越大,相关性越高。
七相关条目假设检验、小概率事件、T检验、抽样
八优缺点优点:检验效率高
缺点:总体分布非正态,且无法通过适当的变量变换达到正态分布,或者分布类型未知,则不能使用;对于分类样本,作用有限。