游程检验
非参数检验是指在总体分布形式未知情况下,可以通过对样本进行检验,以考察总体的分布形式。这是因为在现实问题中,有时不能知道总体服从什么类型的分布,而按照经验或某种理论我们不能对总体进行一些假设,或仅能作一些非常一般性(例如连续分布、对称分布等)的假设,这时候仍用参数检验,其推断出来的结果显然不可信,甚至有可能是错的。所以,必须先对总体的分布做一定的检验,然后才能用参数检验对总体进行推断。
非参数检验的方法,对样本是否来自于正态总体不做严格的限制,而且计算简单;一般非参数检验包含卡方检验、符号检验、秩和检验等检验方法。
非参数检验适用于以下类型的资料:(1)等级资料(有序分类资料)。如疗效按治愈、显效、有效、无效分组的资料;(2)偏态分布资料。当观察值呈偏态或极度偏态分布,而又未经变量变换或虽经变换但仍未达到正态或近似正态分布;(3)分布不明的资料。如新指标分布形态不明,小样本,但不趋向正态分布资料;(4)各组方差明显不齐,且不易变换达到齐性;(5)组内个别观察值偏离过大的资料。(6)开口分组资料。数据分组某一端或两端无明确数值的资料,只给出一个下限或上限,而没有具体数值,如大于等于60岁等。
非参数检验的特点:(1)主要优点是不受总体分布的限制,适用范围广;(2)对适宜用参数统计检验的资料,若用非参数检验处理,会损失部分信息,降低统计检验效率,即犯第二类错误的概率比参数检验大;(3)对于适合参数统计检验条件的资料或变量变换后适合于参数统计检验,最好使用参数检验。当资料不具备用参数检验的条件时,非参数检验是很有效的分析方法。
1.1算法摘要
游程检验也称为“连贯检验”,是根据样本标志表现排列所形成的游程的多少进行判断的检验方法,用来检验变量的取值在一定程度下是否是随机的。其中,游程是指样本序列中连续出现相同变量值的次数。样本变量值通过计算游程数的出现数量,出现太少或太多的游程表明:相应变量值的出现在一定程度上存在非随机性。
1.2.算法原理
游程检验方法:
1、检验总体分布是否相同
将从两个总体中独立抽取的两个样本的观察值混合后,观察游程个数,进行比较。
2、检验样本的随机性
将取自某一总体的样本的观察值按从小到大顺序排列,找出中位数(或均值,或其他指定方式),分为大于中位数的小于中位数的两个部分。用上下交错形成的游程个数来检验样本是否随机。
3、对小样本(n<20)的检验规则
游程检验需查表得到在一定置信水平下的临界值。下面以La和Lb分别表示查表得到的值的上下限。
观察到的游程个数r0≤La或者r0≥Lb,拒绝原假设H0,接受备择假设H1;反之观察到的游程个数满足La<r0<Lb时,接受原假设H0。
4、对大样本(n>20)的检验规则
对大样本的检验,由于样本大,游程数近似于正态分布,可用统计量Z来检验,检验的公式为:
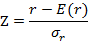
其中: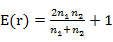 ,
, 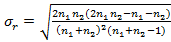
游程检验用来检验变量值出现的随机性,可用于任何领域的数值型数据的检验。例如:设某样本n=12,分别表示男女,有下列的排列:
(1)男\男、女\女\女、男、女\女、男\男\男\男
(2)男\男\男\男\男\男\男、女\女\女\女\女
(3)男、女、男、女、男、女、男、女、男、女、男\男
以r表示序列的游程个数,则上面三个序列的游程数分别为:r=5 ,r=2, r=11
可以看出(1)是随机性序列;(2)(3)是非随机性序列。所以可以用游程的个数来检验样本的随机性或总体的分布特征。
四参考资料1马克威分析系统使用教程,www.tenly.com
2《应用多元分析(第三版)》,王学民编著,上海财经大学出版社
3《游程概率统计原理及其应用》,马秀峰,科学出版社2011年版
五实例在一场比赛中,裁判的公正性是众多球迷关心的一大话题;对一场比赛,按出示黄牌的顺序得出观察序列,其中1表示对甲队出示黄牌,0表示对乙队出示黄牌。通过游程检验,判断这位裁判出示黄牌的行为是否为随机的?
示例数据:1,0,1,1,0,1,1,0,1,0,0,1,1,0,0,0,1,0,1,0,1,0,0,0,0,1,1,1
计算上述数据的游程数:r=17,频数n1=14,n2=14,代入计算Z得到Z=0.5777,同时显著性水平P=0.5634>0.05;故接受原假设,认为裁判出示黄牌是随机的,没有偏袒哪一只队伍。
六输入输出输入变量变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
输出结果:取值的实际频数、游程数、Z值和显著性水平。
七相关条目随机性、抽样、假设检验
八优缺点优点:游程检验事先不确定样本是否服从什么分布,只是根据样本数据的特点检验其随机性,应用范围广、简便、易掌握;
缺点:检验效率较低。