判别分析
统计,顾名思义即将信息统括起来进行计算的意思,它是对数据进行定量处理的理论与技术。统计分析,常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中,分析是最重要的一个环节,如果缺少这一步,会降低统计工作的作用;准确的说,没有统计分析,统计的工作就没有活力、没有发展,也就没有统计工作的意义。
采用统计分析方法进行研究,必须遵循以下几个统计学基本特征:(1)科学性;(2)直观性;(3)可重复性
统计分析除了基础的统计分析外,还包含了高级统计的知识。高级统计一般包括:回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息,还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多,但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题,所以应遵循一定的分析技巧,统计分析技巧可以按照“定性—定量—定性”的顺序,巧妙的将定量分析和定性分析结合。
1.1.算法摘要
判别分析又称为线性判别分析(Linear Discriminant Analysis)是利用已知类别的样本建立判别模型,为未知类别的样本判别其归类的一种统计方法。
判别分析的特点是根据已掌握的、历史上每个类别的若干个样本的数据信息,总结出客观事物分类的规律,建立判别公式和判别准则。当遇到新的样本点时,只要根据总结出来的判别公式和判别准则,就能判别该样本点所属的类别。同时判别分析按照判别的组数来区分,可以分为两组判别分析和多组判别分析。
1.2.算法原理
判别分析的任务是根据已掌握的分类明确的样本,建立较好的判别函数,使产生错判的事例最少,进而对给定的新样本,判断它来自哪个总体。
根据资料的性质,分为定性资料与定量资料的判别分析;采用不同的判别准则,又有费歇尔(Fisher)、贝叶斯(Bayes)、距离判别等判别方法。
费歇尔判别的思想是投影,使多维问题化为一维问题来处理。选择一个适当的投影轴,使所有样本点都投影到该轴,并得到一个投影值。同时要保证:类内的投影值所形成的类内离差尽可能小,类间的投影值所形成的类间离差尽可能大。
贝叶斯判别的思想是根据先验概率求出后验概率,并根据后验概率分布做出统计推断。所谓先验概率是指用概率描述人们事先对所研究的对象的认识的过程;后验概率就是根据具体资料、先验概率、特定的判别规则所计算出来的概率,它是对先验概率修正后的结果。
距离判别的思想是根据样本各样品与各母体之间的距离远近做出判断。即根据资料建立关于各母体的距离判别函数式,将各样本数据逐一代入计算,得出各样本与各母体之间的距离值,把样品归为距离最近的母体。
下面给出费歇尔判别与距离判别的计算公式:
(1)fisher’s 法
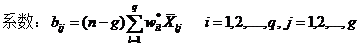
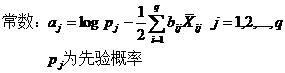
(2)距离判别法
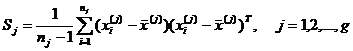
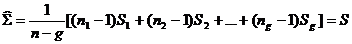
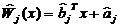
其中 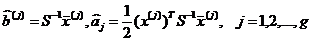
判别分析又称为线性判别分析,产生于20世纪30年代,是利用已知类别的样本建立判别模型,为未知类别的样本判别的一种统计方法。
最早产生的fisher’s判别法,产生于1936年,该算法主要思想是通过将多维数据投影到某个方向上,投影的原则是将总体与总体之间尽可能的放开,然后再选择合适的判别规则,将新的样品进行分类判别。
三相关应用判别分析在自然科学、社会学及经济管理学等学科中都有广泛的应用,例如:动植物分类,医学疾病诊断,社区种类划分,气象区域(或农业气象区)的划分,商品等级分类,职业能力分类,以及人类考古学中的年代归属及人种分类等问题。
在医学疾病诊断中,要根据就诊者的各项症状、体征及化验指标,做出就诊者是否患有某种疾病或某种疾病的哪一类型判断;也可用于环境监测中,根据对某地区的环境污染的综合测定结果判别该地区属于哪一种污染类型等。
四参考资料1.维基百科;
2.百度;
3.MBA智库百科(http://wiki.mbalib.com)
4.马克威分析系统使用教程,www.tenly.com。
5.应用多元分析(第三版),王学民编著,上海财经大学出版社。
五实例示例数据为科学家试图用卫星遥感技术测得地球表面作物的指标,并依此来分辨作物的种类。其中作物1-5分别代表玉米、甘蔗、棉花、大豆和水稻,作物的遥感指标变量包括X1、X2、X3和X4。
| 作物种类 | X1 | X2 | X3 | X4 |
| 1 | 16 | 27 | 31 | 33 |
| 1 | 15 | 23 | 30 | 30 |
| 1 | 16 | 27 | 27 | 26 |
| 1 | 18 | 20 | 25 | 23 |
| 1 | 15 | 15 | 31 | 32 |
| 1 | 12 | 15 | 16 | 73 |
| 2 | 20 | 23 | 23 | 25 |
| 2 | 24 | 24 | 25 | 32 |
| 2 | 21 | 25 | 23 | 24 |
| 2 | 27 | 45 | 24 | 12 |
| 2 | 12 | 13 | 15 | 42 |
| 2 | 22 | 32 | 31 | 43 |
| 3 | 31 | 32 | 33 | 34 |
| 3 | 29 | 32 | 26 | 28 |
| 3 | 34 | 24 | 28 | 45 |
| 3 | 34 | 24 | 28 | 45 |
| 3 | 26 | 32 | 23 | 24 |
| 3 | 52 | 25 | 75 | 26 |
| 3 | 34 | 48 | 25 | 78 |
| 4 | 22 | 23 | 25 | 42 |
| 4 | 25 | 25 | 24 | 26 |
| 4 | 34 | 25 | 16 | 52 |
| 4 | 54 | 23 | 21 | 54 |
| 4 | 25 | 43 | 32 | 15 |
| 4 | 26 | 54 | 2 | 54 |
| 5 | 12 | 45 | 32 | 54 |
| 5 | 24 | 58 | 25 | 34 |
| 5 | 87 | 54 | 61 | 21 |
| 5 | 51 | 31 | 31 | 16 |
| 5 | 96 | 48 | 54 | 62 |
| 5 | 31 | 31 | 11 | 11 |
| 5 | 56 | 13 | 13 | 71 |
| 5 | 32 | 13 | 27 | 32 |
| 5 | 36 | 26 | 54 | 32 |
| 5 | 53 | 8 | 6 | 54 |
| 5 | 32 | 32 | 62 | 16 |
该例子我们用逐步选入变量进行检验,判别方法是Fisher判别法。这是因为实际资料中往往含有较多指标,指标之间有的彼此相关,有的指标对判别毫无用处;所以在建立判别函数之前,应先进行逐步判别分析,以便筛选出可用的变量。然后通过判别方法的计算公式,计算各遥感指标变量的系数;得到的结果如下:
|
|
1 | 2 | 3 | 4 | 5 |
| X1 | 0.0593 | 0.0814 | 0.1331 | 0.1202 | 0.1798 |
| 常数 | -2.0624 | -2.4644 | -3.8947 | -3.4725 | -5.7767 |
从结果中得出,各类判别函数都只是与指标变量X1有关,而与其他的指标无关,这说明由X1所建立的判别函数具有非常显著性的判别效果。且五类判别函数的表达式为:
F1= -2.0624 + 0.0593 * X1;F2= -2.4644 + 0.0814 * X1;F3= -3.8947+ 0.1331 * X1;F4= -3.4725 + 0.1202 * X1;F5= -5.7767 + 0.1798 * X1;
根据未知样本数据代入判别函数中,取计算结果最大的一类,并把该样本点归为此类。
六输入输出输入变量类型:要求数值型变量;如整型、浮点型、布尔型(注:输入变量中必须要有分组变量)
输入数据尺度:标量型
输出结果:判别函数的各类系数以及分类结果。
七相关条目Fisher判别法、距离判别法、贝叶斯判别
八优缺点1.优点
1) 判别分析方法简单、直观,并且易于计算。
2) 一般对于线性可分的样本,总能找到一个投影方向,使得降维后样本仍然线性可分,
3) Fisher判别法可可直接求解权向量;
2.缺点
1) 判别分析必须要有一个学习集,也即要事先知道有哪些类别,而且有相应的分类数据,这样通过已知的分类数据建立一个分类的准则,如果学习集不存在,则无法使用判别分析;
2) 距离判别中,给出的估计通常偏低,没有考虑误判的损失;若将样本分为训练样本和验证样本,需要大样本,并且在构造判别函数时,只用了部分数据样本,损失了过多有价值的信息;
3) Fisher无法对线性不可分的样本进行分类。